7034. Порталы

Некоторые планеты галактики, куда недавно переехал Петя Пяточкин, соединены порталами. Если планеты A и B соединены, это означает, что на каждой из планет стоит специальное устройство – портал – для телепортации между ними. Существо, которое входит в портал на планете A, мгновенно оказывается на планете B и наоборот.

Один и тот же самый портал нельзя использовать для телепортации на разные планеты. Если между парой планет еще нет соединения, их можно соединить, только лишь построив на каждой их них по новому порталу. Строительство порталов стребует немалых затрат и может стоить по-разному на разных планетах.

Будем говорить, что между двумя планетами существует путь телепортации, если с одной планеты можно попасть на другую, телепортировавшись один или несколько раз (используя промежуточные планеты). К сожалению, пока еще не между каждыми двумя планетами существует путь телепортации.

Имея схему имеющегося сообщения планет и зная стоимость портала на каждой планете, определите, какую наименьшую сумму денег нужно потратить, чтобы обеспечить существование пути телепортации между каждой парой планет галактики.

Вход. В первой строке задано два натуральных числа: количество планет галактики n (n ≤ 1000) и количество пар m планет, непосредственно соединенных между собой порталами.

Во второй строке перечислены n натуральных чисел p₁, p₂, …, p_n – стоимости строительства нового портала соответственно на первой, второй, …, n-ой планете. Ни одна из стоимостей не превосходит 10⁶.

В каждой из следующих m строк записано по два натуральных числа a_i и b_i (1 ≤ a_i < b_i ≤ n, 1 ≤ i ≤ m), которые задают пару соединенных между собой планет. Каждую пару записано во входных данных только один раз.

Выход. Выведите наименьшую сумму денег, которую необходимо потратить на строительство на некоторых планетах порталов, чтобы между каждыми двумя планетами, между которыми не было пути телепортации, такой путь был создан.

Пример входа 1	Пример выхода 1
4 2 7 4 7 3 1 3 2 4	10
Пример входа 2	Пример выхода 2
8 5 3 7 5 7 8 12 6 9 4 5 5 6 8 7 1 2 3 1	19

РЕШЕНИЕ

графы – поиск в глубину

Анализ алгоритма

Входной граф может быть несвязным. Выделим в нем компоненты связности. Новые порталы будем строить так, чтобы они соединяли вершины из разных компонент связности. При этом если у нас изначально имеется k компонент, то достаточно построить k – 1 новых связей чтобы граф сделать связным.

Рассмотрим две различные компоненты связности. Для создания перехода между ними необходимо в каждой из них выбрать вершину для построения портала. Поскольку выгоднее строить портал там, где это дешевле всего, то таковыми должны быть самые дешевые вершины в каждой из компонент связности. С другой стороны, поскольку нам необходимо соединить k различных компонент, дешевле всего все компоненты присоединять к той компоненте связности, в которой находится самая дешевая вершина.

Таким образом, следует для каждой компоненты связности найти самую дешевую вершину для постройки портала. Далее среди этих вершин найти ту, которая имеет наименьшую стоимость – в ней будут строиться порталы, ведущие во все остальные связные компоненты.

Пример

В первом тесте граф содержит две компоненты связности. Возле каждой вершины запишем стоимость построения портала в ней.

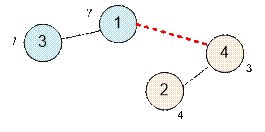
Соединим порталами планеты 1 и 4. Стоимость соединения равна 7 + 3 = 10.

Рассмотрим второй тест. Возле каждой вершины запишем стоимость построения портала в ней.

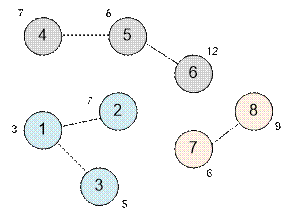
Всего имеется три компоненты связности, значит достаточно построить два новых ребра, или 4 портала (по 2 для каждого ребра). Вершина с номером 1 имеет наименьшую стоимость, следовательно эти два ребра будут выходить из нее. И ребра будут идти в вершины минимальной стоимости каждой из остальных компонент связности.

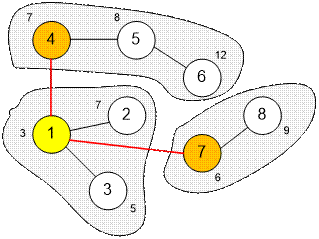
Стоимость соединения планет равна (3 + 7) + (3 + 6) = 19.

Реализация алгоритма

Объявим рабочие глобальные массивы. Граф храним в списке смежности g. Стоимость постройки портала в вершине v находится в cost[v]. В mn[i] будем находить минимальную стоимость постройки портала среди вершин i-ой компоненты связности.

#define MAX 1002

int cost[MAX], used[MAX], mn[MAX];

vector<vector<int> > g;

Поиск в глубину из вершины v, принадлежащей cnt-ой компоненте связности. Проходим по всем вершинам компоненты и ищем в mn[cnt] наименьшую стоимость постройки портала.

void dfs(int v)

{

used[v] = 1;

mn[cnt] = min(mn[cnt], cost[v]);

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (!used[to]) dfs(to);

}

}

Основная часть программы. Читаем входные данные. Строим граф.

scanf("%d %d",&n,&m);

g.resize(n+1);

for(i = 1; i <= n; i++)

scanf("%d",&cost[i]);

for(i = 1; i <= m; i++)

{

scanf("%d %d",&u,&v);

g[u].push_back(v);

g[v].push_back(u);

}

Для каждой компоненты связности cnt запускаем поиск в глубину. Ищем вершину с наименьшей стоимостью постройки портала, найденную стоимость заносим в mn[cnt].

for(i = 0; i < MAX; i++) mn[i] = MAXVALUE;

for(cnt = 0, i = 1; i <= n; i++)

if (!used[i]) dfs(i), cnt++;

Всего граф содержит cnt компонент связности. В переменной temp ищем вершину с наименьшей стоимостью построения портала – минимум среди всех значений mn[0], …, mn[cnt – 1]. В переменной res найдем сумму этих минимумов.

int temp = MAXVALUE;

for(res = i = 0; i < cnt; i++)

{

if (mn[i] < temp) temp = mn[i];

res += mn[i];

}

Пусть, например, минимум temp достигается в j-ой компоненте связности (temp = mn[j]). Тогда общая сумма построения порталов res для всех новых переходов составит

(mn[j] + mn[0]) + … + (mn[j] + mn[j – 1]) + (mn[j] + mn[j + 1]) + …

+ (mn[j] + mn[cnt – 1]) =

= mn[j] * (cnt – 1) + mn[0] + … + mn[j – 1] + mn[j + 1] + … + mn[cnt – 1] =

= temp * (cnt – 2) + mn[0] + … + mn[cnt – 1]

res += temp * (cnt - 2);

Выводим ответ.

printf("%d\n",res);